L3 Transient Conduction
Module Description
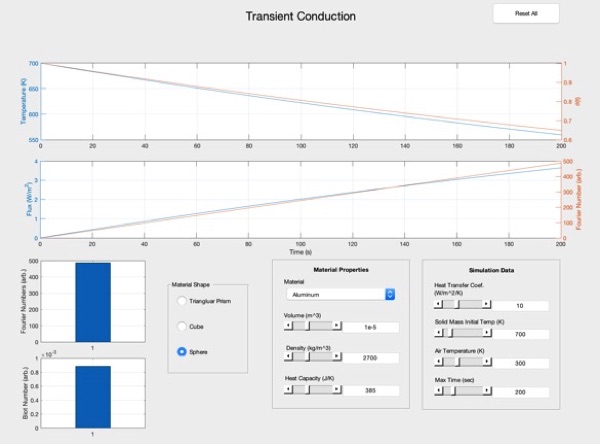
The transient conduction module computes the time-variant, lumped capacitance heating/cooling of an object of pre-defined shape and material. Temperature, heat flux, and Fourier number histories are calculated and Biot number is calculated for establishing validity of the lumped capacitance assumption.
Module Development Theory
Transient, Lumped Capacitance Conduction-Theory
1. Motivation
In consideration of transient, rather than steady state conduction problems, one must consider both spatial and temporal gradients of temperature within a solid body. Approximate, analytical solutions to the problem of 1-D transient conduction can be contrived within regular geometries (e.g. plane walls, cylinders, and spheres) using separation of variables and series approximations. Other analytical methods such as the one-term approximation method, Heisler charts, or Laplace transforms may also be used. For irregular geometries and 2-D or 3-D heat transfer effects, heat transfer is typically numerically solved using finite difference stencils combined with explicit or implicit solvers.
However, for bodies undergoing transient conduction in which temperature gradients within the spatial domain are very small in comparison to temperature gradients in the temporal domain, one can assume that heat conduction within a body is infinitely fast and is controlled exclusively by heat transfer across the surface interface of the object (e.g. convection or radiation). In cases such as this, a simple analytical solution to transient heating of a body can be contrived. Such an analysis is termed a lumped capacitance analysis.
2. The Lumped Capacitance Solution
While infinite conduction is not physically possible, the situation is approximated, for example in convective heating/cooling of a body as shown in Fig. 1, when the thermal resistance to conduction, 
, within an object is much smaller than the thermal resistance to heat transfer at the object's surface, 
.
, within an object is much smaller than the thermal resistance to heat transfer at the object's surface, . 
Fig. 1. Consideration of the internal and external (surface) resistance to heat flow during transient heat transfer to/from a body.
The ratio of these two thermal resistances are termed the Biot number, Bi,
, (1)where 
is a geometry-specific characteristic length dimension of the object, k is the thermal conductivity of the object, 
is the object's exterior surface area, and h is a convective heat transfer coefficient. For low Biot numbers, conductive thermal resistance within the object is much lower than that of heat transfer at the surface and heat transfer within the object will occur much faster than at the interface. Conversely, for high Biot numbers, internal heat transfer thermal resistance is dominant and heat transfer within the object occurs slower than at the object's surface. As a general rule of thumb, a lumped capacitance analysis is considered to be valid if the Biot number of the heat transfer situation is below 0.1.
is a geometry-specific characteristic length dimension of the object, k is the thermal conductivity of the object, is the object's exterior surface area, and h is a convective heat transfer coefficient. For low Biot numbers, conductive thermal resistance within the object is much lower than that of heat transfer at the surface and heat transfer within the object will occur much faster than at the interface. Conversely, for high Biot numbers, internal heat transfer thermal resistance is dominant and heat transfer within the object occurs slower than at the object's surface. As a general rule of thumb, a lumped capacitance analysis is considered to be valid if the Biot number of the heat transfer situation is below 0.1.In consideration of the solution by lumped capacitance of a transient heating/cooling problem, we consider the situation by which an object at an initial temperature, 
is placed in a bath of temperature 
for times t > 0, as shown in Fig. 2. The bath in this example is hotter than the initial temperature of the object (
) and is considered to have infinite thermal mass (i.e. the bath is constant temperature). Assuming the Biot number of the situation is low, we can assume spatial temperature gradients within the object are negligible.
is placed in a bath of temperature for times t > 0, as shown in Fig. 2. The bath in this example is hotter than the initial temperature of the object () and is considered to have infinite thermal mass (i.e. the bath is constant temperature). Assuming the Biot number of the situation is low, we can assume spatial temperature gradients within the object are negligible. 
Fig. 2. Transient convective heating of an object initially at by an infinite thermal mass fluid at .
by an infinite thermal mass fluid at .Starting with an energy balance around the object, 
, and assuming no energy generation, we can write a conservation of energy equation,
, and assuming no energy generation, we can write a conservation of energy equation,
(2.a)
. (2.b)In this equation, ρ,V, and c are the density, volume, and specific heat of the body. Changing variables by letting
(3.a)
, (3.b)and rearranging terms, we can write (2.b) as
. (4)Separating and integrating both sides of this differential equation from time t=0 to arbitrary time, t,
, (5)we get the solution,
(6)or
. (7)Eqtn. (7) gives the temperature, T(t) of an object with initial temperature, and thermal properties ρ, V, and c heated or cooled convectively in an environment having temperature of and convective heat transfer coefficient of h for a time, t. This equation is valid for heating/cooling of objects having constant thermal properties in situations having Biot numbers less than 0.1. In (7), the parameter grouping, 
is termed the thermal time constant, τ and has units of time. The time constant in lumped capacitance heat transfer is synonymous with the time constant associated with RC-circuit charging/discharging. Recall that for an initially grounded capcacitor within an RC circuit, after charging for a duration of one time constant, the voltage across the capacitor will be 63% of the charge voltage. Likewise, the lumped capacitance time constant can be used to determine how long it takes for an object to heat and cool to a specified temperature. There are several other forms of (7) involving the time constant and also the Biot number and the Fourier number, 
. These alternate expressions are presented in (8). The Fourier number represents the ratio of the depth within a body of thermal diffusivity α to which heat has propagated by time, t, divided by the square of the characteristic dimension of the problem. The Fourier number is a dimensionliss time.
and thermal properties ρ, V, and c heated or cooled convectively in an environment having temperature of and convective heat transfer coefficient of h for a time, t. This equation is valid for heating/cooling of objects having constant thermal properties in situations having Biot numbers less than 0.1. In (7), the parameter grouping, is termed the thermal time constant, τ and has units of time. The time constant in lumped capacitance heat transfer is synonymous with the time constant associated with RC-circuit charging/discharging. Recall that for an initially grounded capcacitor within an RC circuit, after charging for a duration of one time constant, the voltage across the capacitor will be 63% of the charge voltage. Likewise, the lumped capacitance time constant can be used to determine how long it takes for an object to heat and cool to a specified temperature. There are several other forms of (7) involving the time constant and also the Biot number and the Fourier number, . These alternate expressions are presented in (8). The Fourier number represents the ratio of the depth within a body of thermal diffusivity α to which heat has propagated by time, t, divided by the square of the characteristic dimension of the problem. The Fourier number is a dimensionliss time.
(8)Expression (8) can be combined with Newton's law of cooling and integrated in time in order to determine the total amount of heat (Joules) either absorbed or liberated by the body:
. (9)3. Simulator Operation
The simulator calculates lumped capacitance heating of a selectable shape object. The simulator calculates object surface area, volume, and
3. Putting it all together
The following is a default set of parameters which, when the included Matlab LiveScript is executed (script distribution), will execute the simulator.
Volume=0.0001; % m^3
Shape=3; % Immersed Shape (3=sphere)
Material=5; % Steel Material
h=600.0; % Convenction Coefficient (W/(k*m^2))
Lump_Temp=1000.0; % Kelvin
Air_Temp=300.0; % Kelvin
Max_Time=300.0; % Seconds
plot_basic(Volume,Shape,Material,h,Lump_Temp,Air_Temp,Max_Time);