Visibility-based Target-tracking Games
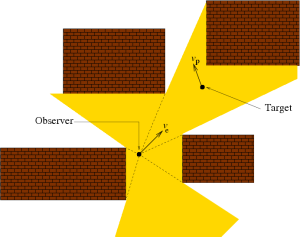
The art gallery problem or museum problem is a wellknown visibility problem in computational geometry. It originates from a real-world problem of guarding an art gallery with the minimum number of guards who together can observe the whole gallery. We consider the problem in which a mobile pursuer attempts to maintain visual contact with an evader as it moves through an environment containing obstacles. This surveillance problem is a variation of traditional pursuit-evasion games, with the additional condition that the pursuer immediately loses the game if at any time it loses sight of the evader.
|
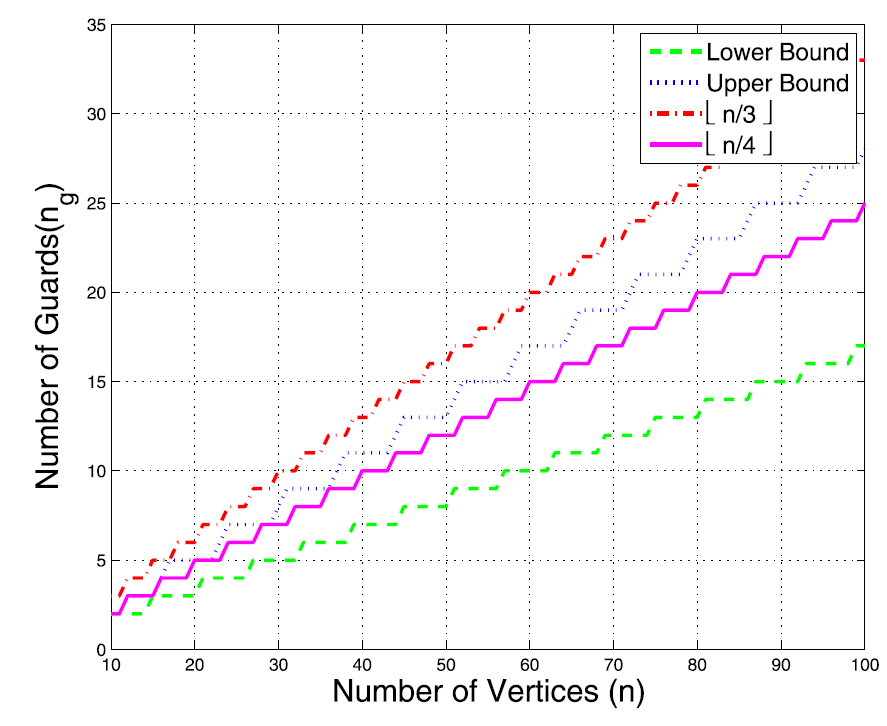
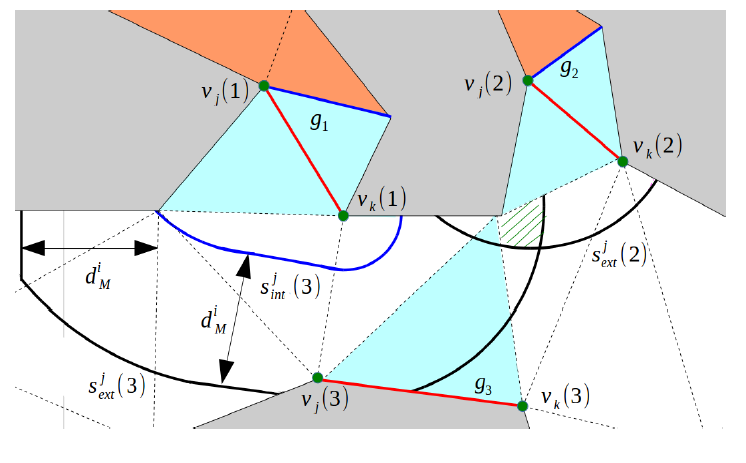
This paper deals with a variant of the art gallery problem in which guards are deployed to track a mobile intruder. We consider a team of free guards equipped with omnidirectional cameras deployed to track a bounded speed intruder inside a simply connected polygonal environment. We present a partitioning technique for any simply connected polygon using its diagonals such that each partition is at most a nonagon. Next, we propose an event-triggered strategy for a single guard to track an intruder around a reflex vertex. Based on the proposed strategy, we formulate the problem of finding the minimum speed of the guard and its corresponding trajectory inside any partition as a convex-optimization problem. The solution to the convex-optimization problem provides an upper bound on the speed of the mobile guard required for persistent tracking of the mobile intruder. Furthermore, we show that the number of guards deployed by the proposed technique belongs to O(2n/7 ) and Ω( n/6 ), which is strictly less than [n3 j (sufficient and sometimes necessary number of guards required for coverage). Finally, we extend the analysis to orthogonal polygons, and show that the upper bound on the number of guards deployed for tracking is strictly less than [n/4 j which is sufficient and sometimes necessary for the coverage problem. |
|
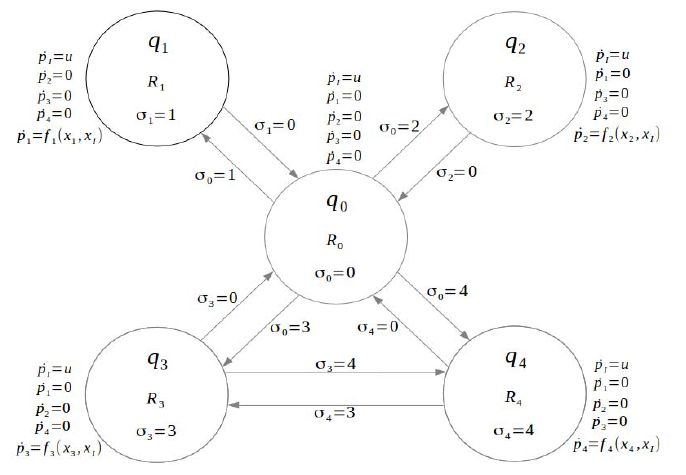
We investigate a variation of the art gallery problem in which a team of mobile guards tries to track an unpredictable intruder in a simply-connected polygonal environment. The guards are deployed based on the strategy initially proposed in [1] which restricts them to move along a specific diagonal within the environment. However, the intruder can move freely within the environment. We define critical regions to generate event-triggered strategies for the guards. Additionally, a hybrid automaton is designed to model the problem, and sufficient conditions are presented for [n/4] guards for persistent surveillance. Guillermo Laguna and Sourabh Bhattacharya Hybrid System for Target-Tracking on Triangulation Graphs. In IEEE International Conference on Robotics and Automation, pg 460-465, 2017.[PDF] |
|
We investigate a variation of the art gallery problem in which a team of mobile guards tries to track an unpredictable intruder in a simply-connected polygonal environment. The guards are confined to move along the diagonals of a polygon, and are deployed according to the strategy proposed in [1] that provides an upper bound of ⌊ n/4 ⌋ mobile guards to cover a simply-connected polygonal environment. We introduce the concept of critical regions to generate event-triggered strategies for the guards. Based on these strategies, we present sufficient conditions for ⌊ n/4 ⌋ guards to track an unpredictable mobile intruder forever. |
|
In this work, we address a visibility-based target-tracking problem in which a mobile observer tries to track a mobile target for a finite time. In order to ensure tracking guarantees for the observer, we formulate the problem as a finite-horizon zero-sum game between the observer and the target. First, we use optimal control theory in conjunction with geometric techniques to solve the problem around a corner. We show that the solution to the optimal control problem for both players is in Nash equilibrium. Next, we partition the visibility polygon of the pursuer and evader based on the winner of the game. These are the projections of the escape set and capture set on the workspace. Finally, we use the partition to construct a region that bounds the set of initial positions of the observer from which it can track the target in an environment containing multiple obstacles for the prespecified time horizon. |
|
|
In this paper, we address the problem of decentralized visibility-based target tracking for a team of mobile observers trying to track a team of mobile targets. Based on the results of previous work, we present the notion of pursuit fields around a single corner. We use the pursuit fields to generate navigation strategies for a single observer to track a single target in general environments. We extend this problem to the scenario when multiple observers and targets with incomplete communication graph are present. We propose a two level hierarchical approach. At the upper level, each observer is allocated to a target through a local minimum cost matching. At the lower level, each observer computes its navigation strategy based on the results of the single observer-single target problem, thereby, decomposing a large multi-agent problem into several 2-agent problems. Finally, we evaluate the performance of the proposed strategy in simulations and experiments. |
|
In this paper, we address the problem of visibility-based target tracking for a team of mobile observers trying to track a team of mobile targets. Based on the results of previous work, the notion of pursuit fields around a single corner is introduced. We use the pursuit fields to generate navigation strategies for a single observer to track a single target in general environments. In order to tackle the case when more than one observer or target is present in the environment, we propose a two level hierarchical approach. At the upper level, the team of observers use a ranking and aggregation technique for allocating each target to an observer. At the lower level, each observer computes its navigation strategy based on the results of the single observer-single target problem, thereby, decomposing a large multi-agent problem into several 2-agent problems. Finally, we present a scalable algorithm that can accommodate an arbitrary number of observers and targets. The performance of this algorithm is evaluated based on simulation and implementation. |
|
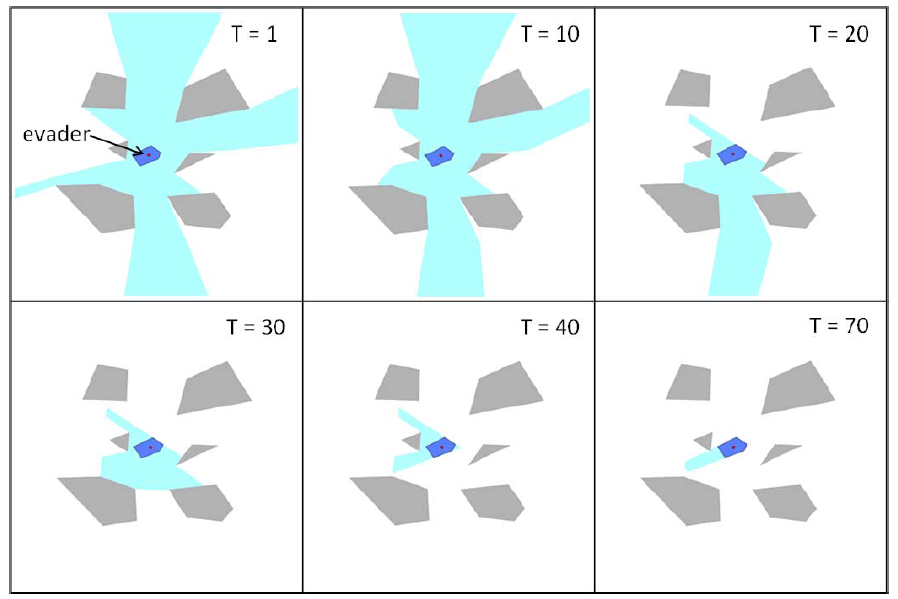
This work addresses a vision-based target tracking problem between a mobile observer and a target in the presence of a circular obstacle. The task of keeping the target in the observer’s field-of-view is modeled as a pursuit-evasion game by assuming that the target is adversarial in nature. Due to the presence of obstacles, this is formulated as a game with state constraints. The objective of the observer is to maintain a line of-sight with the target at all times. The objective of the target is to break the line-of-sight in finite amount of time. First, we establish that the value of the game exists in this setting. Then we reduce the dimension of the problem by formulating the game in relative coordinates, and present a discretization in time and space for the reduced game. Based on this discretization, we use a fully discrete semi-Lagrangian scheme to compute the Kruzkov transform ˇ of the value function numerically, and show that the scheme converges for our problem. Finally, we compute the optimal control action of the players from the Kruzkov transform ˇ of the value function, and demonstrate the performance of the numerical scheme by numerous simulations. |
|
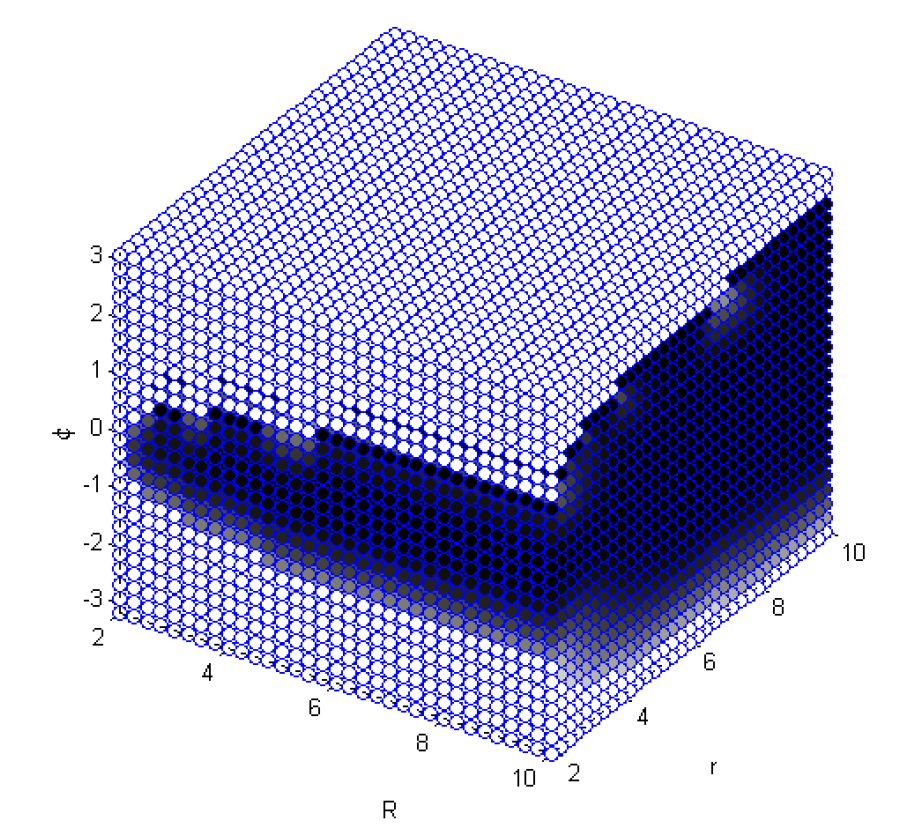
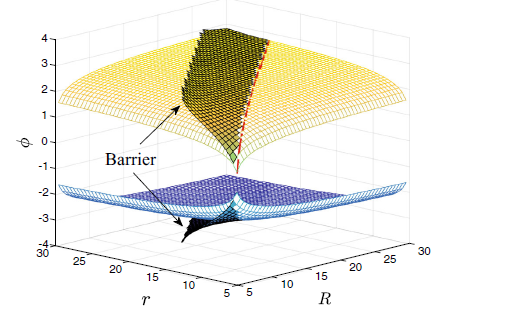
In this paper, we address a visibility-based target tracking game for the scenario when the environment contains a circular obstacle. The game is originally formulated in four dimensions, but due to the symmetry of the environment, the dimension of the state space can be reduced to three. The control policies of the players on possible barrier surfaces are computed on the basis of semipermeability of the barriers. A standard surface, that can be a barrier, is constructed using Isaacs’ techniques. It is shown that the surface lies outside the game space. This opens up the possibility that the evader might be able to win the underlying game of kind for all initial positions in the game space or that the set of such win positions does not coincide with the game space and is determined by some barrier surfaces, construction of which may represent an independent difficult problem. We present the construction of the optimal control policies, and trajectories for the players near the usable part on the terminal manifold by analyzing a related game of degree. |
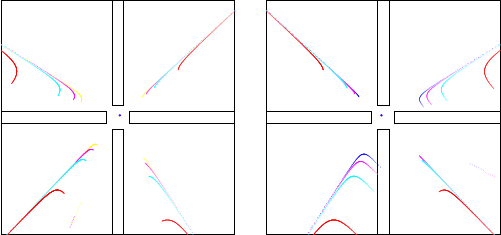
|
In this paper, we analyze a connectivity maintenance problem that arises when two mobile autonomous agents navigate in an environment containing obstacles. Using the Rician fading model for the communication channel, we address the problem for the case in which the motion strategies for one of the agents is assumed to be adversarial in nature. We investigate a specific kind of singular surface that appears in the solution to the pursuit-evasion game, called the dispersal surface. We present the construction of the projection of the dispersal surfaces for various obstacle geometries by fixing the initial position of the evader. Finally, we present numerical simulation for specific environments containing obstacles. |
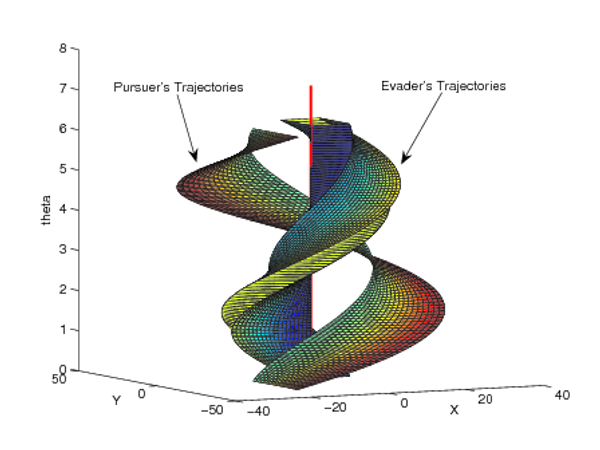
|
In this paper, we present a game theoretic analysis of a visibility based pursuit-evasion game in a planar environment containing obstacles. The pursuer and the evader are holonomic having bounded speeds. Both the players have a complete map of the environment. Both the players have omnidirectional vision and have knowledge about each other's current position as long as they are visible to each other. The pursuer wants to maintain visibility of the evader for maximum possible time and the evader wants to escape the pursuer's sight as soon as possible. Under this information structure, we present necessary and sufficient conditions for surveillance and escape. We present strategies for the players that are in {\it{Nash Equilibrium}}. The strategies are a function of the {\it{value}} of the game. Using these strategies, we construct a value function by integrating the {\it{adjoint equations}} backward in time from the termination situations provided by the corners in the environment. From these value functions we recompute the control strategies for the players to obtain optimal trajectories for the players near the termination situation. As far as we know, this is the first work that presents the necessary and sufficient conditions for tracking for a visibility based pursuit-evasion game and presents the equilibrium strategies for the players. |
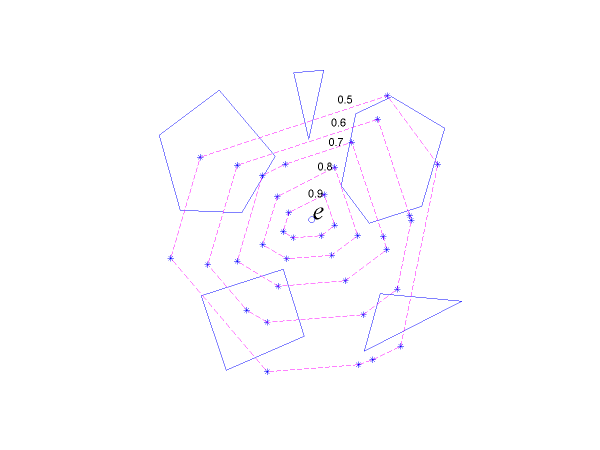
|
It has been shown that the problem of deciding whether or not the pursuer is able to maintain visibility of the evader is at least NP-complete, we present schemes to approximate the set of initial positions of the pursuer from which it might be able to track the evader. We first consider the case of an environment containing only polygonal obstacles. We prove that in this case the set of initial pursuer configurations from which it does not lose the game is bounded. Moreover, we provide polynomial time approximation schemes to bound this set. We then extend our results to the case of arbitrary obstacles with smooth boundaries. Finally, we provide a sufficient condition for surveillance. |
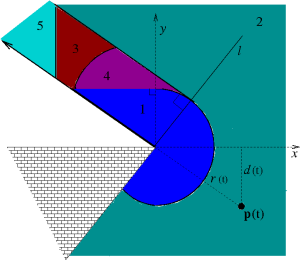
|
We address the problem of surveillance in an environment with obstacles. We show that the problem of tracking an evader with one pursuer around one corner is completely decidable. The pursuer and the evader have complete information about each other's instantaneous position. The pursuer has complete information about the instantaneous velocity of the evader. We present a partition of the visibility region of the pursuer where based on the region in which the evader lies, we provide strategies for the evader to escape the visibility region of the pursuer or for the pursuer to track the target for all future time. We also present the solution to the inverse problem: given the position of the evader, the positions of the pursuer for which the evader can escape the visibility region of the target. These results have been provided for varying speeds of the pursuer and the evader. Based on the results of the inverse problem we provide an $O(n^{3}\log{n})$ algorithm that can decide if the evader can escape from the visibility region of a pursuer for some initial pursuer and evader positions. Finally, we extend the result of the target tracking problem around a corner in two dimensions to an edge in three dimensions. |
|
This paper addresses the pursuit-evasion problem ofmainaining surveillance by a pursuer of an evader in a world populated by polygonal obstacles. This requires the pursur to plan colision-free motions that honor distance constrants imposed by sensor capabilities, while avoiding occlusion of the evader by any obstacle. The paper extends the three-dimensional cellular decomposition ofSchwartz and Sharir to represent the four-dimensional configuration space of the pursuer-evader system, and derive necessary conditions for surveillance (equivalently, sufficient conditions for escape) in terms of this new representation A game theoretic formulation of the problem is then given, and this formulation is used to characterize optimal escape trajectories for the evader A shooting algorithm is proposed thatfinds these trajectories using the minimun prnciple. Finally, noting the similarities between this surveillance problem and the problem of cooperative manipulation by two robots, several cooperation strategies are presented that maximize system performance for cooperative motions. |